0. Intro
지난번에 이어 이번에는 MOSFET에 흐르는 전류 공식을 유도해보겠습니다.
우선 기억해야할 것은 MOSFET은 마치 Capacitor 같은 기능이 있습니다. Gate에 +전압을 가해주면 절연체인 oxide를 사이에 두고 gate에는 홀이, substrate에는 전자가 모이기 때문입니다.
1. Drain Current

①$V_{ds}<V_{gs}-V_{th}$ 경우
drain에 흐르는 전류를 구하기 위해서 다음 2가지 공식을 이용할 것입니다.
$$Q = CV\\ I = Q·v$$
우선 channel에 모이는 전하량을 $Q = CV$로 구해보겠습니다.
이 때 유의할 점이 있습니다.
지난 글에서 Drain전압을 증가시키면 channel이 Drain쪽으로 갈 수록 얇아지다가 전압이 더 증가하면 channel이 끊기는 pinch off에 대해 설명했었습니다.
즉 전하량은 $x$축(channel의 length방향)에 따라 값이 바뀝니다. 따라서 저희는 $x$의 함수인 단위 길이당 전하량을 구해보겠습니다.

gate의 단위 length당 capacitance를 $C$ , 그리고 단위면적당 gate의 capacitance를 $C_{ox}$라 하겠습니다.
그럼 $C = WC_{ox}$가 성립합니다.
그러면 source쪽의 전하량은 $WC_{ox}(V_{gs}-V_{th})$ 입니다.
($V$가 $ V_{gs}-V_{th} $인 이유는 $ V_{gs} < V_{th}$이면 mobile charge가 없기 때문입니다.)
하지만 저희가 궁금한 것은 $x$축에 따른 전하량입니다.
source에서 drain으로 갈수록 channel의 potential에 의해 $V_{gs}-V_{th}$보다 작은 값을 $WC_{ox}$에 곱해주어야 합니다. channel의 potential을 $V(x)$라 하면 $x$축에 따른 단위 길이당 전하량 $Q(x)$는 다음과 같습니다.
$$Q(x) = WC_{ox}[V_{gs}-V(x)-V_{th}]$$
이제는 $ I = Q·v$로 전류를 구해보도록 하겠습니다.
반도체 물성에서 배웠던 공식을 이용하여 전자의 속도를 아래와 같이 구할 수 있습니다.
($\mu_{n}$은 전자의 mobility, $E$ 는 전기장입니다.)
$$v = -\mu_{n}E \\= +\mu_{n}\frac{dV}{dx}$$
$ I = Q·v$에 위에서 구한 $Q(x), v$를 대입해주면 다음과 같습니다.
$$I_{D} = WC_{ox}[V_{gs}-V(x)-V_{th}]\;\mu_{n}\frac{dV(x)}{dx}$$
이 전류는 $x$값과 무관하게 고정입니다.
위 식을 다음과 같이 변형해주고
$$I_{D}\;dx = WC_{ox}[V_{gs}-V(x)-V_{th}]\;\mu_{n}dV(x)$$
양변을 $x$는 $0$~$L$에 대해, $V(x)$는 $0$~$V_{DS}$에 대해 적분 해주면
$$\int_{x=0}^{x=L} I_{D}\;dx = \int_{V(x)=0}^{V(x)=V_{ds}} WC_{ox}[V_{gx}-V(x)-V_{th}]\;\mu_{n}dV(x)$$
$$\therefore I_{D} = \frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}[2(V_{gs}-V_{th})V_{ds}-V_{ds}^{2}]$$
그리고 이 전류는 $V_{ds}= V_{gs}-V_{th} $일 때 최대값
$$I_{D, max} = \frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}(V_{gs}-V_{th})^{2}$$
을 가집니다.

②$V_{ds}>V_{gs}-V_{th}$ 경우
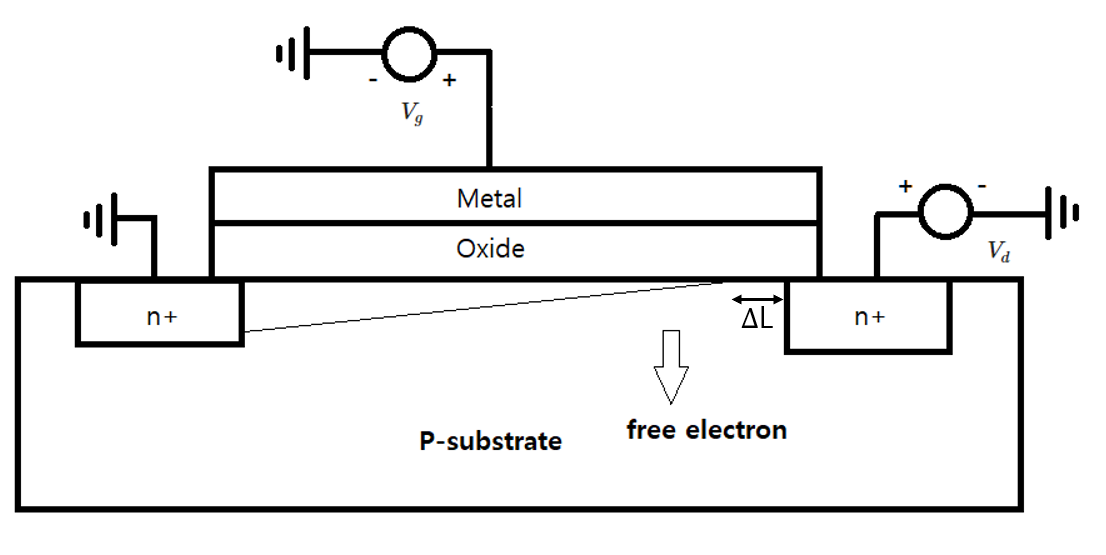
pinch off 가 발생한 경우입니다.
이 경우도 위에서 전류 공식을 유도한 것과 별 차이는 없습니다. 다만 channel의 length가 $L$에서 $L-\Delta L$로 바뀌게되어 적분 구간이 $x$축은 $0$ ~ $L-\Delta L$,
$V(x)$는 $0$ ~ $V_{gs}-V_{th}$로 바뀝니다.
$$I_{D} = \frac{1}{2}\mu_{n}C_{ox}\frac{W}{L-\Delta L}(V_{gs}-V_{th})^{2}$$
보통 $L= L-\Delta L$로 가정합니다.
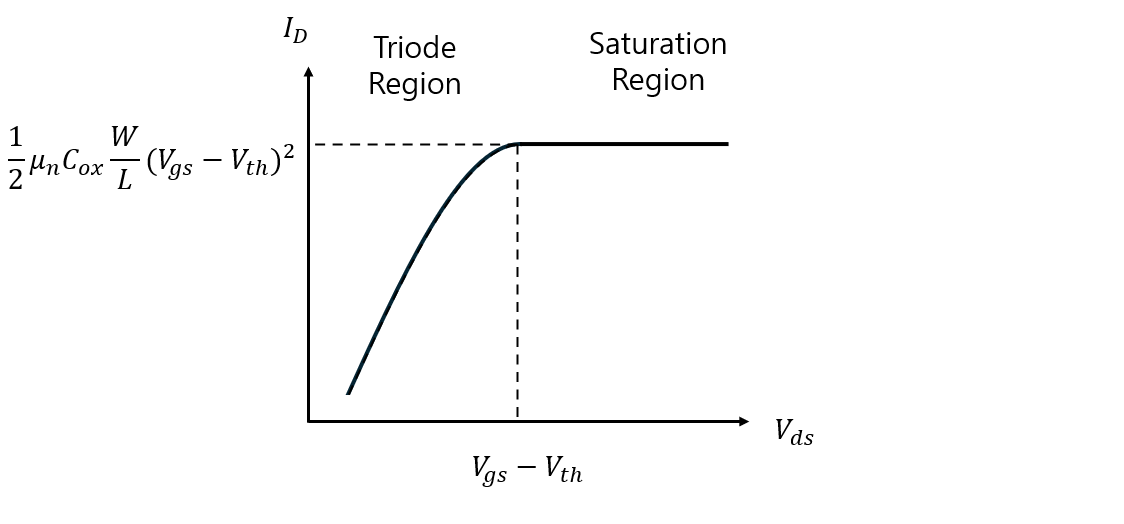
정리하면 그림5와 같이 나타낼 수 있습니다.
Saturation Region의 전류 공식 $I_{D} = \frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}(V_{gs}-V_{th})^{2}$는 꼭 암기하시길 바랍니다.
③Special Case : $V_{ds}<<V_{gs}-V_{th}$ 경우
$$ I_{D} = \frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}[2(V_{gs}-V_{th})V_{ds}-V_{ds}^{2}]$$
이 식에서 $ V_{ds}^{2}\simeq 0$이라고 할 수 있습니다. 그러면
$$ I_{D} = \mu_{n}C_{ox}\frac{W}{L}(V_{gs}-V_{th})V_{ds}$$
즉 $\frac{1}{ \mu_{n}C_{ox}\frac{W}{L}(V_{gs}-V_{th})}$가 일종의 저항이라고 할 수 있겠습니다.
2. MOSFET Nonideality : Channel Length Modulation(CLM)
방금 위에서 $L= L-\Delta L$로 가정을 해 $V_{ds}\geq V_{gs}-V_{th}$이면 전류가 일정하다고 했습니다.
하지만 실제로 그렇지 않고 $V_{ds}$가 증가함에 따라 전류가 미세하게 증가합니다. BJT의 Early Effect와 비슷하다고 할 수 있겠네요.
원래 계산식을 가져오면
$$I_{D} = \frac{1}{2}\mu_{n}C_{ox}\frac{W}{L-\Delta L}(V_{gs}-V_{th})^{2}$$
여기서 $\frac{1}{L-\Delta L} = \frac{1}{L(1-\frac{\Delta L}{L})} = \frac{1}{L} (1+\frac{\Delta L}{L})$이라 할 수 있습니다.
(테일러 급수 $\frac{1}{1-x}=1+x+x^{2}+x^{3}$ ⋯을 이용합니다. $x$가 굉장히 작아 2차항 부터 무시합니다.)
즉 전류식은 다음과 같이 표현할 수 있습니다.
$$I_{D} = \frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}(V_{gs}-V_{th})^{2}(1+\frac{\Delta L}{L} )$$
$\Delta L$은 $V_{ds}$에 비례합니다. 따라서 비례상수 $k$를 사용하여 다시 표현하면
$$I_{D} = \frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}(V_{gs}-V_{th})^{2}(1+\frac{k V_{ds}}{L} )$$
$\frac{k}{L}=\lambda$라고 하면
$$\therefore I_{D} = \frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}(V_{gs}-V_{th})^{2}(1+\lambda V_{ds})$$
이것이$V_{ds}$가 생긴, saturation region에서의 조금 더 정확한 전류식입니다.
$\lambda \propto \frac{1}{L}$ 즉 $\lambda$는 CLM이 얼마나 일어나는가를 판단하는 지표라고 할 수 있겠습니다.
직관적으로 $L$이 크면 $\Delta L$이 발생해도 그 영향이 작다고 이해하시면 됩니다.
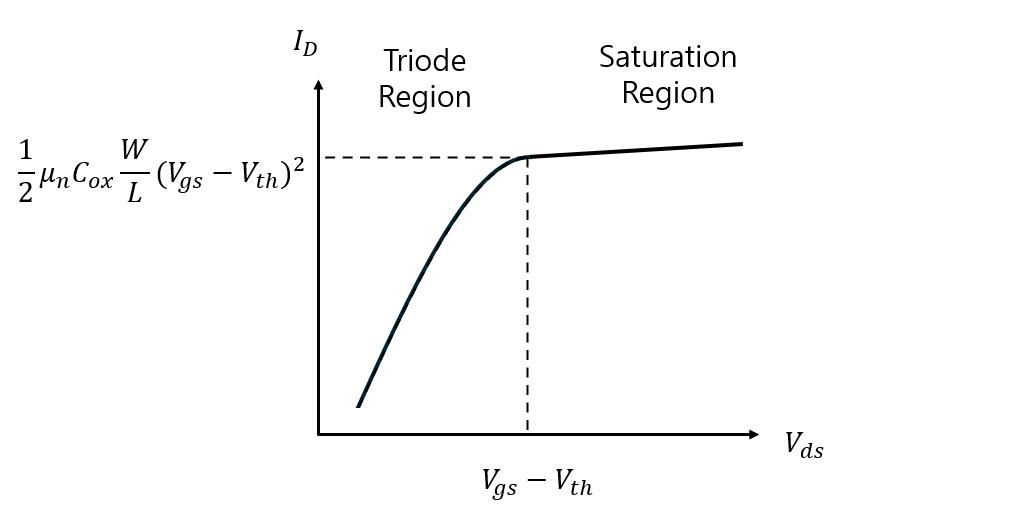
그림6와 그림5를 비교하면 Saturation region에서 기울기가 다르다는 것을 알 수 있습니다.
$\lambda$가 커질수록 기울기도 증가하게 됩니다.
오늘은 여기까지 포스팅 하겠습니다.
Saturaion Region의 전류 공식은 꼭 암기하시길 바랍니다.
질문, 오류지적 환영합니다.
'전자회로' 카테고리의 다른 글
| 5. CMOS Amplifier - Common Source Amplifier, small signal analysis (0) | 2024.08.03 |
|---|---|
| 4. MOSFET, Small Signal Model (0) | 2024.07.30 |
| 3-1. MOSFET (0) | 2024.07.19 |
| 2. BJT(Bipolar Junction Transistor) (1) | 2024.07.14 |
| 1. PN Junction (PN 접합) (1) | 2024.07.09 |