14. Transfer Function, Bode Plot

0. Intro

안녕하세요 오랜만입니다. 그동안 바빠서 글을 못썼었네요

 

오늘은 Transfer Function과 Bode Plot에 대해 알아보겠습니다.

 

 

1. Transfer Function

그림1.

그림1과 같은 회로가 있다고 가정해보겠습니다.

 

그럼 Vout은 어떻게 구할까요?

그림2.

그림2 처럼 Laplace 변환을 통해 구하면 Voltage Dividing으로 구하면 훨씬 쉽죠?

 

그러면

$\Large V_{out}(s)=V_{in}(s)\times \Huge\frac{\frac{1}{sC}}{\Large R+\Huge\frac{1}{sC}}$

이렇게 표현할 수 있습니다.

 

이걸 한번 더 정리하면

$\Large \frac{V_{out}(s)}{ V_{in}(s) }=\Huge\frac{\frac{1}{sC}}{\Large R+\Huge\frac{1}{sC}}$

 

여기서

$\Large \frac{V_{out}(s)}{V_{in}(s)}=H(s)$

라고 표현하는데요

 

$H(s)$를 Transfer function 이라고 합니다.

입력과 출력의 관계를 표현하는 함수라서 그렇게 불리는거죠.

 

$\large s=j\omega=j2\pi f$ 입니다.

 

즉 저 transfer function은 주파수에 대한 함수이죠 

 

이 transfer function을 x축을 주파수축 , y축을 저 함수의 크기로 나타낸 것을 Bodeplot이라고 합니다.

 

x축은 log scale로 합니다.

 

y축은 저 transferfunction에 $log$를 취하고 20을 곱한 dB(데시벨)을 사용합니다.

 

소리가 몇 dB이다 할 때 그 dB입니다. $log$를 취하고 20을 곱해주면 dB가 됩니다.

 

만약 저 Transferfunction의 크기가 특정 주파수에서 100이다 그러면 그 주파수에서 Transfer function은 40dB인 겁니다.

 

2. Bode Plot

 

그림2의 transfer function을 보겠습니다.

$$ H(s) = \frac{1}{sRC+1} = \frac{1}{j(2\pi f) RC+1} $$

 

$f_{c} = \frac{1}{2\pi RC}$라 하면

$$H(s) =\Large \frac{1}{1+j(\frac{f}{f_{c}})}$$

가 됩니다.

 

 

 

이 transfer function의 크기를 구해보겠습니다.

$$|H(s)| =\Large \frac{1}{1+(\frac{f}{f_{c}})^2}$$

이 식이 bodeplot의 y축에 들어가는 식이구요 이것이 주파수에 따라 크기가 변하므로 magnitude response라고 합니다.

 

만약

 

a. $f<<f_{c}$

$|H(jf)| \simeq 1$

 

b. $f>>f_{c}$

$|H(jf)| \simeq 0$

 

c. $f= f_{c} $

$|H(jf)|=\Large\frac{1}{\sqrt{2}}$

라고 할 수 있겠죠?

 

이걸 dB로 바꾸면

 

a. $f<<f_{c}$

$|H(jf)| \simeq 0\,dB$

 

b. $f>>f_{c}$

$|H(jf)| \simeq -\infty\,dB$

 

c. $f= f_{c} $

$|H(jf)|= -3\,dB$

라고 할 수 있겠죠?

 

그리고 $f$가 커질 수록 $|H(s)|$가 작아지는 것을 볼 수 있습니다.

 

그럼 우리는 Bodeplot으로 rough하게 이렇게 그릴 수 있습니다.

그림3.

 

그림3 처럼 그릴 수가 있는데요 이 때 magnitude가 -3dB 떨어지는 곳을 corner frequency라고 합니다.$(=f_{c})$

 

3. Pole, Zero

이번에는  transfer function의 일반화한 경우를 보겠습니다.

 

LTI system(Liner, Time-invariant system)에서는 임의의 transfer function은 다음과 같은 형태를 띕니다.

 

$$H(s)=\large A_{o}\Large\frac{(1+\frac{s}{\omega_{z1}})(1+ \frac{s}{\omega_{z2}} ) ⋯ (1+ \frac{s}{\omega_{z3}})}{(1+ \frac{s}{\omega_{p1}})(1+ \frac{s}{\omega_{p2}} ) ⋯ (1+ \frac{s}{\omega_{p3}} )}$$

 

여기서 만약 주파수가 0인 신호에 대한(DC) transfer function은 $H(0)=A_{o}$가 됩니다. 이 떄 $A_{o}$를 DC gain이라고 합니다.

 

그리고 분모를 0으로 만드는 $s$값, 분자를 0으로 만드는 $s$값들을 각각 pole, zero라고 합니다.

 

$ s = -\omega_{p1}, -\omega_{p2}\,⋯\, -\omega_{pk}$    ->   pole

$ s = -\omega_{z1},-\omega_{z2}\,⋯\,-\omega_{zk}$    ->   zero

 

$\omega_{p1}, \omega_{p1} ⋯$ 이런 것들은 pole frequency

$\omega_{z1}, \omega_{z2} ⋯ $ 이런 것들은 zero frequency라고 합니다.

 

4. Bode's Rule

그림3과 같은 Bodeplot을 그릴 때 쉽게 그리기 위한 대략적인 규칙이 있습니다.

 

$f$가 각 pole frequency를 지날 때마다 magnitude는 20dB/dec 씩 감소합니다.

$f$가 각 zero frequency를 지날 때마다 magnitude는 20dB/dec 씩 증가합니다.

이런 규칙은 계산을 통해 나온 것이며 아마 회로이론때 배우셨을 겁니다.

 

 

예시) 

$$H(jf) = 1000 \frac{(1+\frac{jf}{10k})}{(1+\frac{jf}{100})(1+\frac{jf}{1M})}$$

 

위의 transfer function의 경우를 보겠습니다.

pole frequency는 100 ,1M이고

zero frequency는 10k입니다.

 

이 frequency들 사이에서 bodeplot을 그려보겠습니다.

case 1) $f<<100$

 

$H(jf)=1000$로 근사 할 수 있습니다.

그림4.

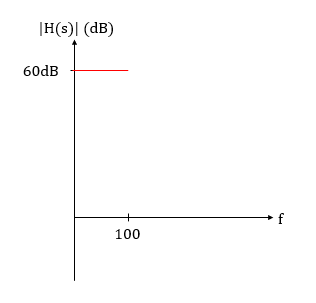
그럼 그림 4처럼 대략적으로 그릴 수 있습니다.

(f가 100 근처의 작은 값이어도 대략적인 개형을 파악하기 위해 이렇게 그립니다)

 

 

case 2) $100<<f<<10K

$$H(jf)= 1000\frac{1}{(1+\frac{jf}{100})}$$

로 근사할 수 있습니다.

그럼 다음과 같이 그림5를 그릴 수 있습니다.

그림5.

100에서 pole frequency이므로 20dB/decade씩 감소하여 10k에서는 20dB가 됩니다.

마찬 가지로 100과 10k 근처에서도 대략적인 개형을 위해 근사한 transfer function을 본 것입니다.

 

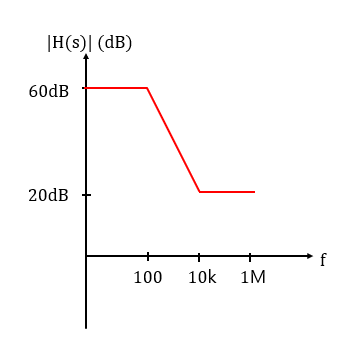
case 3) $10k<<f<<1M$$

 

$$H(jf)= 1000(1+\frac{jf}{10k})$$

로 근사할 수 있습니다.

10k는 zero frequency라 20dB/dec씩 증가합니다. 하지만 그림5 에서 20dB/dec씩 감소하고 있었습니다.

 

그래서 그림6 처럼 10k부터 1M까지는 일직성형태가 됩니다.

그림6

case 4) $1M<f

$$H(jf) = 1000 \frac{1}{(1+\frac{jf}{1M})}$$

로 근사할 수 있습니다.

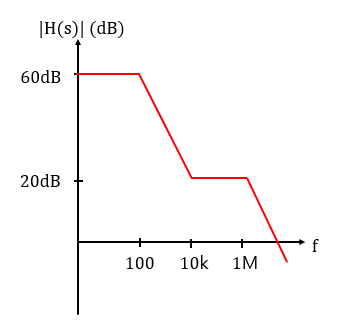
1M은 pole frequency이므로 20dB/dec씩 감소합니다.

따라서 그림7처럼 최종적으로 bodeplot을 그릴 수 있습니다.

그림7.

5. Phase

transfer funciton의 frequency에 따른 phase도 그릴 수 있습니다.

 

이 역시 회로이론에서 배운 내용에 기반하므로 자세한 증명은 생략하고

 

어떤식으로 그리는지 알려드리겠습니다.

 

zero frequency의 1/10지점과 10배 지점 사이에서 phase는 감소하고

1/10지점에서 zero frequency에서 45도, zero frequency지점에서 10배지점에서 45도 감소합니다.

 

pole frequency는 같은 원리로 phase가 증가한다고 생각하면 됩니다.

 

위 transfer function을 예시를 들면

그림8.

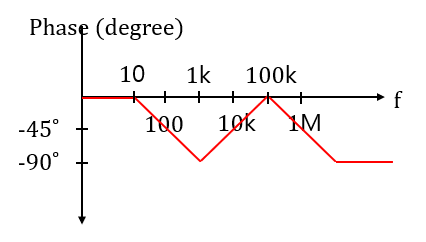
그림8 처럼 예시를 들을 수있습니다.

 

당연히 대략적인 그림이지만 큰 개형은 비슷합니다. 100K에서는 input과 output 신호의  phase변환이 없고 1K에서는 phase가 90도 뒤처지는 transfer function입니다. 이런식으로 해석하면 됩니다.

 

질문 오류지적 환영합니다.